
자료실
곡선 구간의 교량방수 & 교면방수 보수 면적 계산법 - 로드팜건설
-
조회수 : 979
|
2018-07-16 22:40:25

안녕하세요. 교면방수 및 교량방수 시공회사 로드팜건설입니다.
이번 포스팅은 곡선 구간의 교면방수 및 교량방수 보수 면적을 계산해 보겠습니다.
교량의 푹은 39m이며 중앙분리대는 1m, 인도는 3m(편도), 교량의 직선 길이는 200m로 설정하겠습니다. 이를 그림으로 그려보면 아래의 그림과 같이 나옵니다.
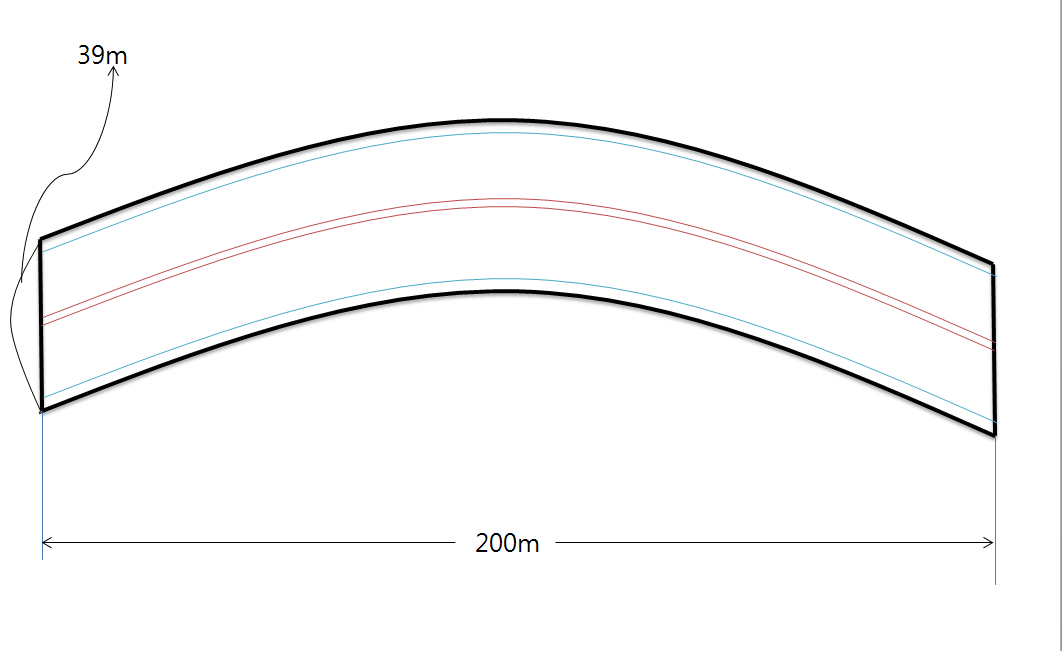
그림을 해석해보면, 교량의 직선길이는 200m이고, 폭은 39m라는 것을 확인할 수 있습니다. 또한, 가운데에 빨간선은 중앙분리대를 표현한 것입니다. 중앙분리대의 폭은 1m입니다. 교량의 위, 아래에 있는 파란 선은 인도를 표현한 것입니다. 양쪽 인도의 폭은 각 3m씩입니다. 교량방수의 면적은 전체 교량의 면적에서, 중앙분리대의 면적과 양쪽 인도의 면적을 빼주면 됩니다. 수학적으로 계산해보면, 각 부분의 넓이는 평형하는 곡선들로 인해 생겼다고 볼 수가 있습니다. 그래서 좌표평면위의 이차함수를 이용해서 교면방수를 해야할 면적을 구해보겠습니다.
우선 좌표평면 위에서의 함수를 설정해야합니다. 위의 교량에서 맨 밑의 두꺼운 검은 선이 (-100, 0), (100, 0)을 지나고 이차항의 계수가 -1인 이차함수라고 가정하겠습니다. 그럼, 이차함수 식은 y = -(x + 100)(x - 100) = -(x²-10000) = -x² + 10000가 됩니다. 맨 밑에 있는 두꺼운 검은 선의 함수를 설정했으니, 나머지 선들도 쉽게 함수를 설정할 수가 있습니다. 바로 위의 인도를 나타내는 파란 선은, 폭이 3m이므로 y = -x²+10000에서 y절편에 3만 더해주면 됩니다. 즉, 아래쪽의 파란선의 식은 y = -x²+10003이 됩니다. 그리고 똑같은 방식으로, 그 위의 곡선들을 구해주면 됩니다. 아래쪽 파란선과 아래쪽 빨간선의 폭은 16m, 빨간 두선의 폭은 1m, 위쪽 빨간선과 위쪽 파란선의 폭은 16m, 위쪽 파란선과 위쪽 진한 검은선의 폭은 3m입니다. 총 6개의 이차함수를 y절편의 차이를 이용해서 구할 수가 있습니다.

위에서부터 6개의 이차함수를 써보면 위의 식과 같습니다. 이제 교면방수할 면적을 구해보겠습니다. 우선, 인테그랄을 이용해서 전체 교량의 넓이를 구해줘야합니다. 그리고 인테그랄을 이용해서 두 인도의 넓이와 중앙분리대의 넓이를 빼주면, 교량방수를 해야할 면적을 구할 수가 있습니다.

총 교량의 면적을 구했으니, 여기서 중앙분리대의 면적과 인도의 면적을 구해 빼주면 됩니다.

총 교량의 면적은 7,800m²이고 두 인도의 면적과 중앙분리대의 면적의 합은 1,200m² + 200m² = 1,400m²이므로
곡선 구간에서 교량방수를 해야할 면적은 7,800m² - 1,400m² = 6,400m²입니다.
곡선 구간의 교량방수 & 교면방수 보수 면적 계산법 - 로드팜건설
- 조회수 : 979 | 2018-07-16 22:40:25

안녕하세요. 교면방수 및 교량방수 시공회사 로드팜건설입니다.
이번 포스팅은 곡선 구간의 교면방수 및 교량방수 보수 면적을 계산해 보겠습니다.
교량의 푹은 39m이며 중앙분리대는 1m, 인도는 3m(편도), 교량의 직선 길이는 200m로 설정하겠습니다. 이를 그림으로 그려보면 아래의 그림과 같이 나옵니다.

그림을 해석해보면, 교량의 직선길이는 200m이고, 폭은 39m라는 것을 확인할 수 있습니다. 또한, 가운데에 빨간선은 중앙분리대를 표현한 것입니다. 중앙분리대의 폭은 1m입니다. 교량의 위, 아래에 있는 파란 선은 인도를 표현한 것입니다. 양쪽 인도의 폭은 각 3m씩입니다. 교량방수의 면적은 전체 교량의 면적에서, 중앙분리대의 면적과 양쪽 인도의 면적을 빼주면 됩니다. 수학적으로 계산해보면, 각 부분의 넓이는 평형하는 곡선들로 인해 생겼다고 볼 수가 있습니다. 그래서 좌표평면위의 이차함수를 이용해서 교면방수를 해야할 면적을 구해보겠습니다.
우선 좌표평면 위에서의 함수를 설정해야합니다. 위의 교량에서 맨 밑의 두꺼운 검은 선이 (-100, 0), (100, 0)을 지나고 이차항의 계수가 -1인 이차함수라고 가정하겠습니다. 그럼, 이차함수 식은 y = -(x + 100)(x - 100) = -(x²-10000) = -x² + 10000가 됩니다. 맨 밑에 있는 두꺼운 검은 선의 함수를 설정했으니, 나머지 선들도 쉽게 함수를 설정할 수가 있습니다. 바로 위의 인도를 나타내는 파란 선은, 폭이 3m이므로 y = -x²+10000에서 y절편에 3만 더해주면 됩니다. 즉, 아래쪽의 파란선의 식은 y = -x²+10003이 됩니다. 그리고 똑같은 방식으로, 그 위의 곡선들을 구해주면 됩니다. 아래쪽 파란선과 아래쪽 빨간선의 폭은 16m, 빨간 두선의 폭은 1m, 위쪽 빨간선과 위쪽 파란선의 폭은 16m, 위쪽 파란선과 위쪽 진한 검은선의 폭은 3m입니다. 총 6개의 이차함수를 y절편의 차이를 이용해서 구할 수가 있습니다.

위에서부터 6개의 이차함수를 써보면 위의 식과 같습니다. 이제 교면방수할 면적을 구해보겠습니다. 우선, 인테그랄을 이용해서 전체 교량의 넓이를 구해줘야합니다. 그리고 인테그랄을 이용해서 두 인도의 넓이와 중앙분리대의 넓이를 빼주면, 교량방수를 해야할 면적을 구할 수가 있습니다.

총 교량의 면적을 구했으니, 여기서 중앙분리대의 면적과 인도의 면적을 구해 빼주면 됩니다.

총 교량의 면적은 7,800m²이고 두 인도의 면적과 중앙분리대의 면적의 합은 1,200m² + 200m² = 1,400m²이므로
곡선 구간에서 교량방수를 해야할 면적은 7,800m² - 1,400m² = 6,400m²입니다.


